Super hydrophobie

De l’angle d’Young à l’effet Fakir (L2/L3).

Introduction

De nombreux exemples de superhydrophobie existent dans la nature. Cette propriété permet notamment aux feuilles de lotus et de ginkgo biloba de rester secs et propres pour transformer plus efficacement le CO2 en dioxygène avec la photosynthèse. Cette même propriété permet à la plupart des oiseaux de décoller directement de l’eau, à quelques exceptions près comme le cormoran, dont les plumes hydrophiles s’imbibent d’eau (raison pour laquelle on le voit perché, se sécher après chaque plongeon).

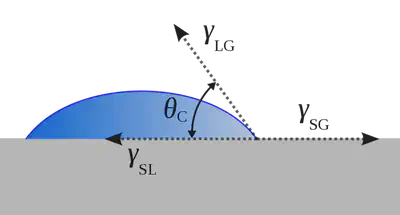
La mesure de l’angle d’Young, défini comme l’angle formée entre une surface et une goutte d’eau posée dessus, permet de caractériser les surfaces hydrophiles des surfaces hydrophobes. Une goutte d’eau posée sur une surface hydrophile, comme le bois, a tendance à épouser la forme de la surface alors que sur une surface superhydrophobe, elle forme une perle. Cette propriété perlante a inspiré la conception de vêtements imperméables comme les K-ways.

Dans la suite, nous nous intéressons aux spores de lycopode, une plante de type fougère apparue il y a 470 millions d’années. Ses spores microscopiques sont superhydrophobes et auraient permis à la plante de peupler la Terre en traversant les océans.

Présentation des spores de Lycopodium

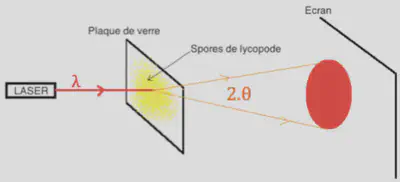
La diffraction de la lumière permet de déterminer la taille des spores. La mesure du diamètre apparent du disque d’Airy $\theta$ illustré dans la Figure 1 permet de remonter à leur diamètre D par la relation $\theta = 1,22 \frac{\lambda}{D}$. Numériquement, on trouve $D\approx 20 \mu m$.

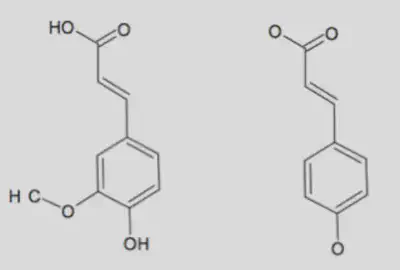
Les spores de lycopode sont recouverts de deux enveloppes, l’une interne appelée endospore, l’autre externe appelée exospore. L’exospore est constitué de sporopollénine, un polymère naturel dont la composition exacte est toujours inconnue car la sporopollénine est très inerte. Cependant, des études ont montré que la structure de la sporopollénine est proche de celle de la $\beta$ carotène, et obtenue à partir d’acide férulique et d’acide p-coumarique [1]. La présence de longues chaînes carbonées expliquerait leur hydrophobie.

L’observation de spores au microscope optique (x100, x400, x600) suggère que leur surface n’est pas lisse. Des irrégularités distantes de quelques $\mu m$ la rendent rugueuse et superhydrophobe. C’est l’effet Fakir: une goutte d’eau ne s’écrase pas sous l’effet de la pesanteur mais laisse sous elle des poches d’air, tel un fakir posé sur des clous. Ceci se produit lorsque la distance entre les irrégularités est inférieure à la longueur capillaire de l’eau $L_c = \sqrt{\frac{\gamma}{\rho g}} \approx 3$ mm.

Tracé d’un diagramme énergétique

Deux gouttes enrobées de spores de lycopode ne coalescent pas, une propriété qui peut servir pour transporter un liquide dans un fluide [2]. En revanche, si une goutte dispose de suffisamment d’énergie, la coalescence peut se produire. Dans [3], les auteurs déterminent la vitesse d’impact critique pour qu’une goutte de rayon variable R traverse une couche de spore. Nous étudierons ici la barrière énergétique que représentent des spores pour la coalescence de gouttes d’eau. Nous considérons des gouttes d’eau de volume constant $\approx \mu m^3 $. On note $R$ leur rayon.

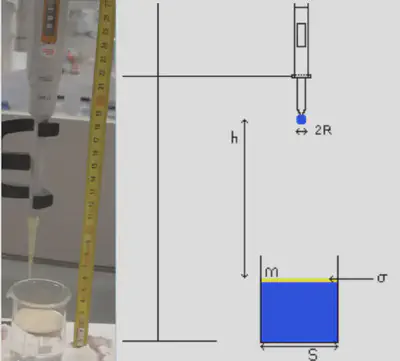
Montage et protocole

Le schéma du dispositif expérimental est illustré dans la Figure 3. $S$ définit la surface du bécher, $m$ la masse de spore déposée et $\sigma = \frac{m}{S}$ la densité surfacique de spores, supposée uniforme à l’échelle du bécher. A $\sigma$ fixée, j’ai fait varier $h$, la hauteur depuis laquelle la goutte d’eau est lâchée sans vitesse initiale, l’interface de spores étant repérée par $h=0$. En première approximation, la vitesse d’impact est $v=\sqrt{2gh}$. Le résultat expérimental est binaire, soit la goutte traverse la surface, soit elle ne la traverse pas.

Etude statistique

A $\sigma$ et h fixées j’ai lâché successivement entre 5 et 10 gouttes. Le résultat est une fraction comprise entre 0 (aucune goutte lâchée n’a traversé les spores) et 1 (toutes les gouttes lâchées ont traversé). Ainsi, à $\sigma$ donnée, en réitérant ce qui précède pour différentes valeurs de h, je définis deux hauteurs $h_{min}$ et $h_{max}$.

Si $h < h_{min}$ la goutte ne traverse jamais et si $h > h_{max}$ la goutte traverse toujours: l’apport d’énergie est suffisant. L’intervalle $[h_{min}-h_{max}]$ correspond aux incertitudes de mesure.

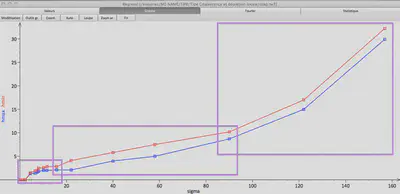
Après plus de 800 gouttes lâchées, j’ai obtenu un diagramme énergétique où $\sigma$ est porté en abscisse, $h_{min}$ et $h_{max}$ en ordonné. On distingue trois domaines. Un premier où $h$ est proportionnelle à $\sqrt{\sigma}$, puis une évolution linéaire et enfin quadratique. On remarque aussi qu’il existe une densité surfacique critique $\sigma_c$. Si $\sigma< \sigma_c$ une goutte d’eau traverse la couche de spores, quelque soit sa hauteur de chute.

Modélisation de la déplétion locale de spores

Enoncé d’un principe

Lorsque la déformation de l’interface est maximale (état repéré par * et dépendant de la hauteur de chute h), si la densité surfacique apparente $\sigma^*$ est inférieure à $\sigma_c$, la goutte traverse. Sinon la goutte ne traverse pas. Le cas limite $\sigma^*=\sigma_c$ correspond à la frontière entre les deux régimes. Pour déterminer $\sigma^*$ en fonction des paramètres $h$ et $\sigma$, je me suis rendu à l’institut d’Alembert de Jussieu pour filmer la déformation. Arnaud Antkowiak, professeur à l’UPMC et chercheur en mécanique des fluides, m’a accueilli et permis de réaliser des videos avec une caméra rapide (plus de 1000 images par seconde).

Modélisation du domaine linéaire

Les séquences photos montrent que dans ce domaine, il n’y a pas de projections de spores. La conservation de la matière se traduit par $$ S^* \sigma^*=S\sigma $$ En première approximation, la surface de spores qui se déforme se situe directement sous la goutte. La variation de la surface est donc donnée par $$ \Delta S = S^* - S \approx \Pi R^2 (\frac{\sigma}{\sigma^*}-1) $$ Par ailleurs, la conservation de l’énergie se traduit par $$ \rho (\frac{4}{3} \pi R^3) gh= \gamma \Delta S $$ où le terme de gauche correspond à l’énergie potentielle de la goutte d’eau lachée, et le terme de droite correspond à la variation d’énergie de surface due à sa déformation. L’équation du diagramme énergétique s’obtient en remplaçant $\sigma^*$ par $\sigma_c$ dans les équations (2) et (3). On obtient bien une relation linéaire entre $h$ et $\sigma$, valable pour $\sigma \geq \sigma_c$ $$ h \approx \frac{4}{3} \frac{\gamma}{\rho Rg} (\frac{\sigma}{\sigma_c}-1) $$ $h$ est propotionnel à $\gamma$ et inversement proportionnel à la masse de la goutte d’eau, cela semble cohérent.

Conclusion

Pour qu’une goutte d’eau traverse effectivement des spores de Lycopode de densité surfacique $\sigma$, il faut un apport d’énergie cinétique suffisant pour permettre une déplétion locale de spores conséquente. Le transfert et l’échange d’énergie sont déterminants dans la nature de la réponse.

Reference

[1] S. Barrier. Physical and chemical properties of sporopollenin exine particles. PhD Thesis. University of Hull. 2008.

[2] P. Aussillous. Les gouttes enrobées. PhD Thesis. Université Paris VI. 2002.

[3] E. Lorenceau, C. Planche, A. L. Biance et al. Coalescence of armored interface under impact. 2013.